Calculadora de Área de Polígono – Coordenadas XY, Fórmula del Zapato, Superficie Irregular

Cómo Calcular el Área de un Polígono con la Fórmula del Zapato: Guía Paso a Paso

La Fórmula del Zapato (también conocida como la fórmula de Gauss o fórmula de los cordones) es una herramienta matemática poderosa y sencilla para calcular el área de un polígono irregular a partir de sus coordenadas XY. 

Esta técnica es ideal para estudiantes, ingenieros y técnicos que trabajan con superficies irregulares, como parcelas de terreno, diseños arquitectónicos o proyectos de ingeniería. 

A continuación, te explicamos cómo usarla de manera clara y práctica.

¿Qué es la Fórmula del Zapato?

La Fórmula del Zapato DEFINITION La Fórmula del Zapato permite calcular el área de un polígono tomando las coordenadas de sus vértices (x₁, y₁), (x₂, y₂), …, (xₙ, yₙ). Se basa en sumar productos cruzados de las coordenadas de los vértices, organizados en un orden específico (generalmente en sentido antihorario). La fórmula es:

Área = ½ | Σ (xᵢyᵢ₊₁ – yᵢxᵢ₊₁) |

Donde el sumatorio se realiza sobre todos los vértices del polígono, y el último vértice se conecta al primero para cerrar el ciclo. El valor absoluto asegura un resultado positivo.

Paso a Paso para Usar la Fórmula del Zapato

1. Lista las coordenadas en orden: Enumera las coordenadas (x, y) de los vértices del polígono en orden antihorario. Si no conoces el orden, asegúrate de ser consistente (por ejemplo, siempre en sentido antihorario).
2. Organiza las coordenadas: Escribe las coordenadas en una tabla, repitiendo el primer vértice al final para cerrar el polígono.
3. Calcula los productos cruzados: Multiplica cada xᵢ por yᵢ₊₁ (la y del siguiente vértice) y suma todos los resultados. Luego, multiplica cada yᵢ por xᵢ₊₁ (la x del siguiente vértice) y suma esos resultados.
4. Resta y divide: Resta la suma de los productos xᵢyᵢ₊₁ menos la suma de los productos yᵢxᵢ₊₁, toma el valor absoluto y divídelo por 2 para obtener el área.
5. Convierte unidades si es necesario: Si las coordenadas están en metros, el área estará en metros cuadrados. Convierte a otras unidades (como pies cuadrados) usando factores de conversión (1 m² = 10.7639 ft²).

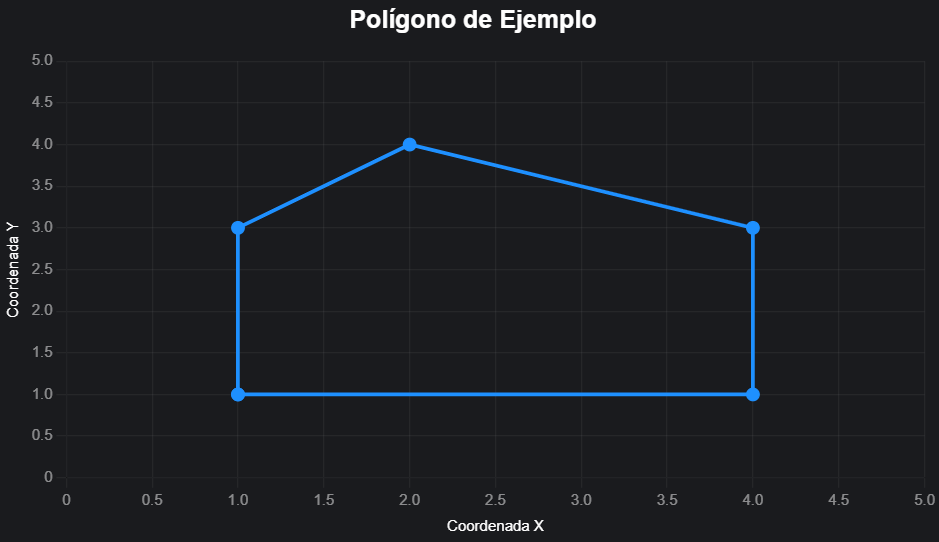
Ejemplo Práctico

Supongamos que tenemos un polígono con los siguientes vértices: (1, 1), (4, 1), (4, 3), (2, 4), (1, 3). Vamos a calcular su área:

1. Lista de coordenadas (en orden antihorario, repitiendo el primer vértice al final):
   
   • (1, 1), (4, 1), (4, 3), (2, 4), (1, 3), (1, 1)
2. Calcula los productos cruzados:
   
   • Suma de xᵢyᵢ₊₁: (1·1) + (4·3) + (4·4) + (2·3) + (1·1) = 1 + 12 + 16 + 6 + 1 = 36
   • Suma de yᵢxᵢ₊₁: (1·4) + (1·4) + (3·2) + (4·1) + (3·1) = 4 + 4 + 6 + 4 + 3 = 21
3. Resta y divide:
   
   • Área = ½ | 36 – 21 | = ½ · 15 = 7.5 metros cuadrados
4. Conversión (opcional): Si necesitas el área en pies cuadrados: 7.5 m² · 10.7639 = 80.72925 ft².

Visualización del Polígono

A continuación, se muestra un gráfico que representa el polígono del ejemplo con sus vértices para ayudarte a visualizar cómo se conectan las coordenadas: