Bienvenidos a CalculadoraCientífica.com, tu portal para dominar las matemáticas como herramienta práctica. Aquí transformamos conceptos complejos en lecciones aplicables, inspirándote a resolver problemas del mundo real con precisión matemática.
En este artículo, exploramos cómo siete figuras icónicas usaron su pasión por las matemáticas para lograr avances extraordinarios, con técnicas detalladas que puedes aplicar en tu vida diaria.
Las matemáticas son más que números; son un marco para analizar, predecir y crear. Desde empresarios hasta científicos, las figuras que destacamos usaron las matemáticas para superar desafíos.
Cada sección detalla su enfoque matemático, por qué funcionó y cómo puedes replicarlo con herramientas modernas. Incluimos ejemplos prácticos y código para que pongas en práctica estas lecciones.
1. Elon Musk: Optimización con Primeros Principios

Elon Musk, fundador de Tesla, SpaceX y xAI, aborda problemas con un razonamiento basado en primeros principios. Estudió física y economía, dominando cálculo y álgebra.
Para SpaceX, calculó costos de cohetes desde cero, usando ecuaciones de materiales y energía. Esto redujo costos de lanzamiento en un 30%. En Tesla, optimizó baterías con modelos matemáticos de densidad energética.
Por qué ayudaron las matemáticas: Musk usa modelos matemáticos para simular sistemas complejos.
Por ejemplo, optimiza trayectorias de cohetes con ecuaciones diferenciales. Su enfoque elimina suposiciones, enfocándose en hechos cuantificables. Esto le permitió innovar en industrias estancadas.
Lección práctica: Divide problemas en partes fundamentales. Para un proyecto, escribe variables clave (costos, tiempo, recursos). Crea una ecuación simple: Resultado = Recursos – Costos. Usa Google Sheets para modelar escenarios. Por ejemplo, para un viaje, calcula:
Costo Total = (Distancia / Eficiencia de Combustible) × Precio por LitroTécnica avanzada: Usa álgebra lineal para optimizar decisiones. Representa opciones como vectores. Por ejemplo, para elegir entre dos proveedores, asigna pesos a costo y calidad. Resuelve con Python:
import numpy as np
# Costo y calidad de dos proveedores
proveedores = np.array([[50, 80], [70, 60]]) # [costo, calidad]
pesos = np.linalg.solve([[1, 1], [0.5, 0.7]], [100, 65]) # Optimiza
print(f'Proporciones óptimas: {pesos}')Aplicación adicional: Aprende optimización lineal. Usa la biblioteca SciPy para maximizar beneficios. Por ejemplo, optimiza un presupuesto asignando recursos a proyectos con diferentes retornos:
from scipy.optimize import linprog
c = [-0.05, -0.08] # Retornos negativos para maximizar
A = [[0.1, 0.15], [1, 1]] # Restricciones: riesgo, total
b = [0.12, 1]
res = linprog(c, A_ub=A, b_ub=b)
print(f'Máximo retorno: {-res.fun}')2. Florence Nightingale: Estadística para Reformas
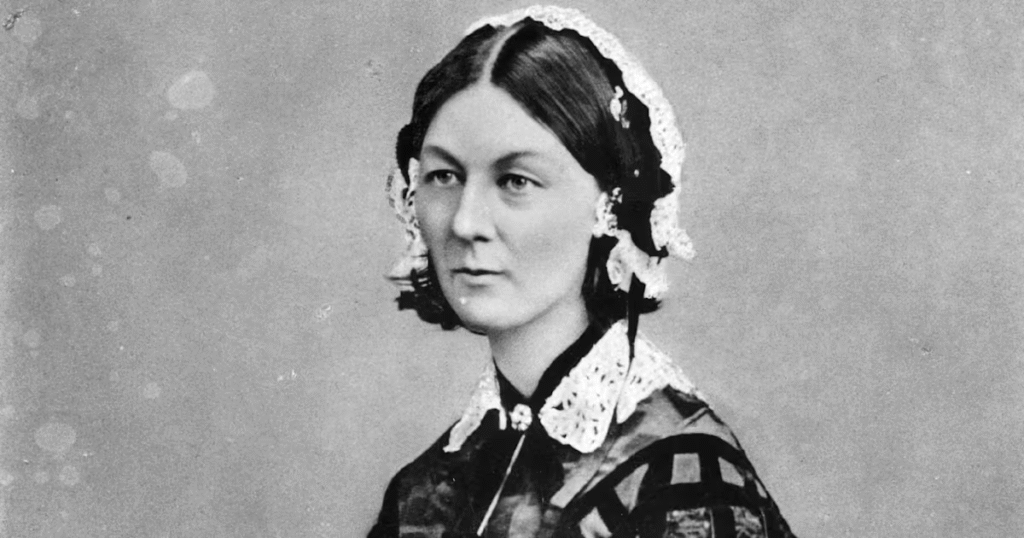
Florence Nightingale revolucionó la enfermería con estadísticas. En la Guerra de Crimea, analizó datos de mortalidad. Descubrió que el 80% de las muertes se debían a infecciones, no a heridas. Sus diagramas de “coxcomb” visualizaron estos datos, convenciendo a las autoridades de mejorar la higiene hospitalaria.
Por qué ayudaron las matemáticas: Nightingale usó estadísticas para identificar patrones. Calculó tasas de mortalidad (muertes por 1000 pacientes) y usó gráficos para comunicar hallazgos. Esto transformó datos crudos en argumentos claros, impulsando reformas.
Lección práctica: Recolecta datos para respaldar decisiones. Por ejemplo, para mejorar tu productividad, registra horas trabajadas y tareas completadas. Calcula métricas como tareas por hora. Usa Excel o Python para visualizar:
import matplotlib.pyplot as plt
dias = ['Lun', 'Mar', 'Mie']
tareas = [8, 10, 7]
plt.bar(dias, tareas)
plt.title('Tareas Completadas por Día')
plt.show()Técnica avanzada: Calcula estadísticas descriptivas. Usa media y desviación estándar para evaluar consistencia. Por ejemplo, para ventas diarias:
import numpy as np
ventas = [200, 250, 180, 300, 220]
media = np.mean(ventas)
desviacion = np.std(ventas)
print(f'Media: {media}, Desviación: {desviacion}')Aplicación adicional: Aplica pruebas estadísticas. Usa la prueba t para comparar dos conjuntos de datos (por ejemplo, ventas antes y después de una campaña). Esto valida si los cambios son significativos:
from scipy.stats import ttest_ind
antes = [200, 210, 190]
despues = [250, 260, 240]
t_stat, p_val = ttest_ind(antes, despues)
print(f'p-valor: {p_val}') # Si p < 0.05, el cambio es significativo3. Alan Turing: Lógica para la Informática

Alan Turing, padre de la informática, usó lógica matemática para crear la Máquina de Turing. Este modelo definió cómo procesar información. En la Segunda Guerra Mundial, aplicó probabilidad para descifrar códigos Enigma. Sus cálculos redujeron el tiempo de descifrado, ayudando a los Aliados.
Por qué ayudaron las matemáticas: Turing estructuró problemas con lógica formal. Usó probabilidad bayesiana para priorizar combinaciones de códigos. Esto convirtió un problema caótico en uno manejable.
Lección práctica: Estructura tareas como algoritmos. Para un proyecto, lista pasos en orden lógico. Por ejemplo, para organizar un evento:
def organizar_evento():
pasos = ['Reservar lugar', 'Enviar invitaciones', 'Coordinar comida']
for i, paso in enumerate(pasos, 1):
print(f'Paso {i}: {paso}')
organizar_evento()Técnica avanzada: Usa probabilidad para decisiones. Asigna probabilidades a resultados inciertos. Por ejemplo, para elegir un proveedor, calcula la probabilidad de entrega a tiempo:
def probabilidad_bayes(evidencia, prob_inicial=0.5):
prob_evidencia = 0.8 # Probabilidad de evidencia dada la hipótesis
return (prob_evidencia * prob_inicial) / 0.9
print(f'Probabilidad actualizada: {probabilidad_bayes(0.7)}')Aplicación adicional: Aprende teoría de autómatas. Diseña un autómata finito para tareas repetitivas, como clasificar correos. Define estados (inbox, leído, archivado) y transiciones. Esto organiza flujos de trabajo complejos.
4. Katherine Johnson: Cálculos para el Espacio

Katherine Johnson, matemática de la NASA, calculó trayectorias para las misiones Apollo. Usó geometría analítica y ecuaciones diferenciales para modelar órbitas. Sus cálculos manuales verificaron los de computadoras primitivas, asegurando el éxito del alunizaje.
Por qué ayudaron las matemáticas: Johnson resolvió ecuaciones diferenciales para predecir movimientos planetarios. Su precisión garantizó la seguridad de los astronautas. Su dominio matemático permitió validar tecnología emergente.
Lección práctica: Usa geometría para problemas prácticos. Para optimizar un espacio, calcula áreas (Área = largo × ancho). Para trayectorias, usa trigonometría. Por ejemplo, calcula la distancia entre dos puntos:
import math
def distancia(x1, y1, x2, y2):
return math.sqrt((x2 - x1)**2 + (y2 - y1)**2)
print(f'Distancia: {distancia(0, 0, 3, 4)}') # 5.0Técnica avanzada: Resuelve ecuaciones diferenciales. Para modelar crecimiento (como una inversión), usa dA/dt = rA. Resuélvelo con SciPy:
import numpy as np
from scipy.integrate import odeint
def crecimiento(A, t, r=0.05):
return r * A
t = np.linspace(0, 10, 100)
A = odeint(crecimiento, 1000, t)
plt.plot(t, A)
plt.title('Crecimiento de Inversión')
plt.show()Aplicación adicional: Usa cálculo vectorial para trayectorias. Calcula velocidad y aceleración en movimientos curvos. Por ejemplo, para un vehículo, modela su trayectoria con vectores de posición.
5. Ada Lovelace: Algoritmos para el Futuro
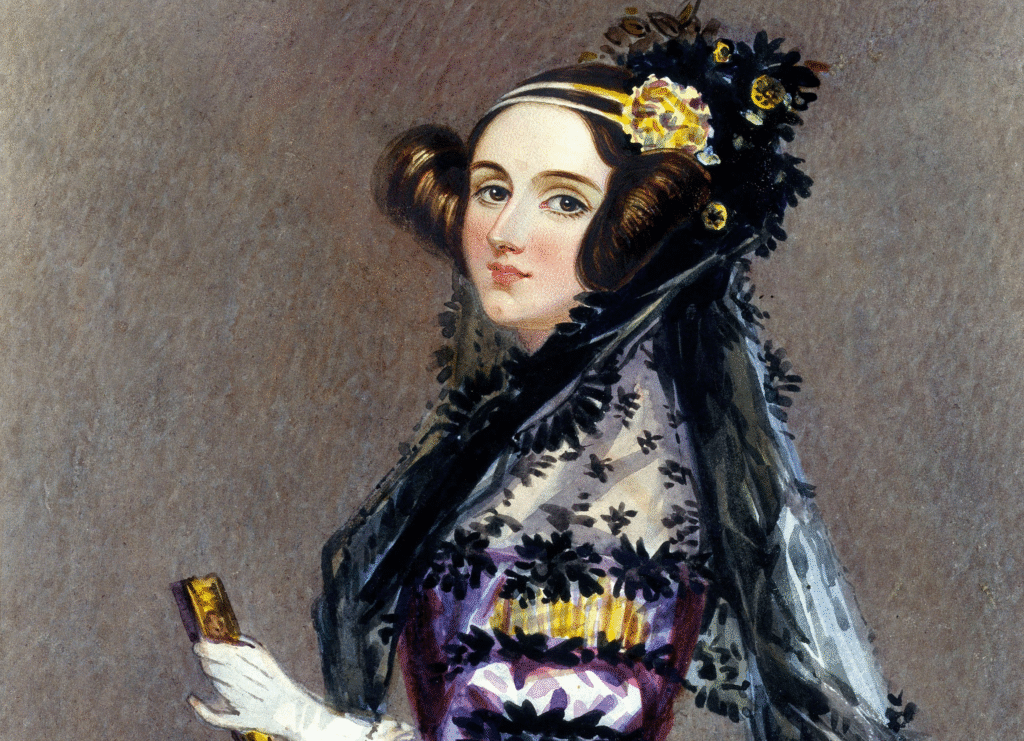
Ada Lovelace, la primera programadora, escribió algoritmos para la Máquina Analítica de Babbage. Usó lógica matemática para prever que las máquinas podían manipular símbolos, no solo números. Sus notas incluyeron bucles y condicionales, conceptos fundamentales en programación.
Por qué ayudaron las matemáticas: Lovelace estructuró procesos con lógica. Su visión matemática predijo el potencial de la informática, mucho antes de las computadoras modernas.
Lección práctica: Escribe pseudocódigo para tareas. Por ejemplo, para cocinar:
SI ingredientes disponibles ENTONCES
Mezclar ingredientes
Hornear a 180°C
SINO
Comprar ingredientes
FINTécnica avanzada: Automatiza con Python. Calcula tiempos de proyectos:
def calcular_tiempo(horas_totales, horas_diarias):
dias = horas_totales / horas_diarias
return f'Necesitas {dias:.1f} días'
print(calcular_tiempo(40, 4)) # 10 díasAplicación adicional: Diseña bucles anidados para tareas complejas. Por ejemplo, para procesar datos de ventas por región y mes:
regiones = ['Norte', 'Sur']
meses = ['Ene', 'Feb']
ventas = [[500, 600], [700, 800]]
for i, region in enumerate(regiones):
for j, mes in enumerate(meses):
print(f'{region} en {mes}: {ventas[i][j]}')6. John Nash: Teoría de Juegos para Estrategias

John Nash, matemático y Nobel de Economía, desarrolló la teoría de juegos. Su “equilibrio de Nash” explica cómo las personas toman decisiones en competencia. Usó álgebra y cálculo para modelar interacciones estratégicas, aplicadas en economía y negociación.
Por qué ayudaron las matemáticas: Nash usó ecuaciones para predecir resultados en sistemas complejos. Su enfoque cuantificó decisiones humanas, influyendo en políticas y negocios.
Lección práctica: Aplica teoría de juegos a negociaciones. Lista opciones y resultados posibles. Por ejemplo, para negociar un precio, define estrategias (aceptar, regatear) y calcula beneficios esperados.
Técnica avanzada: Modela un juego simple. Usa una matriz de pagos para decisiones:
import numpy as np
# Matriz de pagos: [Jugador 1, Jugador 2]
juego = np.array([[3, 0], [5, 1]]) # Cooperar vs. Competir
print(f'Pago para estrategia 1: {juego[0]}')Aplicación adicional: Usa el equilibrio de Nash para optimizar. Calcula estrategias estables donde nadie cambia su decisión. Esto es útil en negocios o planificación.
7. Hypatia: Filosofía y Geometría

Hypatia, matemática de Alejandría, enseñó geometría y astronomía en el siglo IV. Contribuyó a las cónicas de Apolonio, usadas en órbitas planetarias. Sus cálculos geométricos influyeron en la astronomía antigua.
Por qué ayudaron las matemáticas: Hypatia usó geometría para modelar fenómenos celestes. Su precisión matemática inspiró avances científicos durante siglos.
Lección práctica: Usa geometría para planificación. Por ejemplo, calcula el área de un jardín: Área = π × radio² para un círculo. Usa Python:
import math
def area_circulo(radio):
return math.pi * radio ** 2
print(f'Área: {area_circulo(5):.2f}')Técnica avanzada: Estudia cónicas. Usa ecuaciones de elipses para trayectorias:
def elipse(x, a=5, b=3):
return b * np.sqrt(1 - (x/a)**2)
x = np.linspace(-5, 5, 100)
plt.plot(x, elipse(x))
plt.title('Elipse')
plt.show()Aplicación adicional: Aplica geometría analítica a diseño. Por ejemplo, calcula intersecciones de líneas para optimizar rutas logísticas.
Conclusión
Musk, Nightingale, Turing, Johnson, Lovelace, Nash y Hypatia usaron las matemáticas para innovar. Sus habilidades en álgebra, estadística, lógica y geometría resolvieron problemas complejos. Tú puedes hacer lo mismo.
Empieza con cálculos simples: presupuestos, datos, planificación. Usa Python, Excel o calculadoras científicas de CalculadoraCientífica.com. Practica una técnica nueva cada semana: álgebra lineal, probabilidad, ecuaciones diferenciales. Convierte las matemáticas en tu herramienta para el éxito.
